Unidad 2 Generación de variables aleatorias

CLASIFICACIÓN DE LOS NÚMEROS

Números naturalesCon los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).

Números enteros:Losnúmeros enteros son del tipo: = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.

Números reales:
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por R.

Números imaginarios:
Un número imaginario se denota por bi, donde:
b es un número real
i es la unidad imaginaria: √-9= (3i, -3i)
Los números imaginarios permiten calcular raíces con índice par y radicando negativo.
Números complejos:
Un número complejo en forma binómica es a + bi.
El número a es la parte real del número complejo.
El número b es la parte imaginaria del número complejo.
Si b = 0 el número complejo se reduce a un número real, ya que a + 0i = a.
Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
números racionales
cumplen la propiedad arquimediana o de densidad, esto es, para cualquier pareja de números racionales existe otro número racional situado entre ellos, propiedad que no estaba presente en los números enteros, por lo que los números racionales son densos en la recta de los números reales.

Generación de variables aleatorias

Buscamos métodos que nos permitan obtener valores de variables aleatorias que sigan
determinadas distribuciones de probabilidad a partir de los números aleatorios generados, que siguen
la distribución Uniforme en el intervalo

Normalmente existen varios algoritmos que se pueden utilizar para generar valores de una
determinada distribución, y diferentes factores que se pueden considerar para determinar qué
algoritmo utilizar en un caso particular. Desafortunadamente dichos factores suelen entrar en conflicto
unos con otros y a veces se ha de llegar a una solución de compromiso.

Algunos de estos factores son los siguientes:

Exactitud: se han de obtener valores de una variable con una precisión dada. A veces
se tiene suficiente con obtener una aproximación y otras no.

Eficiencia: el algoritmo que implementa el método de generación tiene asociado un
tiempo de ejecución y un gasto de memoria. Elegiremos un método que sea eficiente
en cuando al tiempo y a la cantidad de memoria requeridos.

Complejidad: Buscamos métodos que tengan complejidad mínima, siempre y cuando
se garantice cierta exactitud.

Robusted: el método tiene que ser eficiente para cualquier valor que tomen los
parámetros de la distribución que siga la variable aleatoria.
ü Facilidad de implementación.

LA VARIABLE ALEATORIA

Se denomina variable aleatoria, a una variable X que puede tomar un conjunto de valores {x₀, x₁, x₂, ... x_n-1}, con probabilidades {p₀, p₁, p₂, ... p_n-1}. Por ejemplo, en la experiencia de lanzar monedas, los posibles resultados son {cara, cruz}, y sus probabilidades son {1/2, 1/2}. En la experiencia de lanzar dados, los resultados posibles son {1, 2, 3, 4, 5, 6} y sus probabilidades respectivas son {1/6, 1/6, 1/6, 1/6, 1/6, 1/6}.

Una variable aleatoria (v.a.) X es una función real definida en el espacio muestral asociado a un experimento aleatorio, Ω.

$X:Omegato mathbb R$

Se llama rango de una v.a. X y lo denotaremos R_X, al conjunto de los valores reales que ésta puede tomar, según la aplicación X. Dicho de otro modo, el rango de una v.a. es el recorrido de la función por la que ésta queda definida:

$R_X = {xinmathbb R / exists , omegain Omega : X(omega) = x }$

Variable aleatoria discreta: una v.a. es discreta si su recorrido es un conjunto discreto. La variable del ejemplo anterior es discreta. Sus probabilidades se recogen en la función de cuantía (véanse las distribuciones de variable discreta).

Variable aleatoria continua: una v.a. es continua si su recorrido no es un conjunto numerable. Intuitivamente esto significa que el conjunto de posibles valores de la variable abarca todo un intervalo de números reales. Por ejemplo, la variable que asigna la estatura a una persona extraída de una determinada población es una variable continua ya que, teóricamente, todo valor entre, pongamos por caso, 0 y 2,50 m, es posible.⁶ (véanse las distribuciones de variable continua

Desviación estándar

La desviación estándar o desviación típica (σ) es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.

Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.

Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que representan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones.

La desviación estándar es una medida del grado de dispersión de los datos con respecto al valor promedio. Dicho de otra manera, la desviación estándar es simplemente el "promedio" o variación esperada con respecto a la media aritmética.

Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, cada una tiene una media de 7. Sus desviaciones estándar muestrales son 8,08, 5,77 y 1,33, respectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.

La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio).

Varianza

la varianza (que es el cuadrado de la desviación estándar: σ²) se define así:

Es la media de las diferencias con la media elevadas al cuadrado.

En otras palabras, sigue estos pasos:

1. Calcula la media (el promedio de los números)
2. Ahora, por cada número resta la media y eleva el resultado al cuadrado (la diferencia elevada al cuadrado).
3. Ahora calcula la media de esas diferencias al cuadrado. (¿Por qué al cuadrado?)

Ejemplo

Tú y tus amigos habéis medido las alturas de vuestros perros (en milímetros):

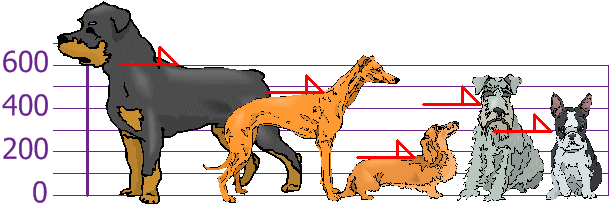
Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.

Calcula la media, la varianza y la desviación estándar.

Respuesta:

Media =	600 + 470 + 170 + 430 + 300	=	1970	= 394

	5		5

así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:

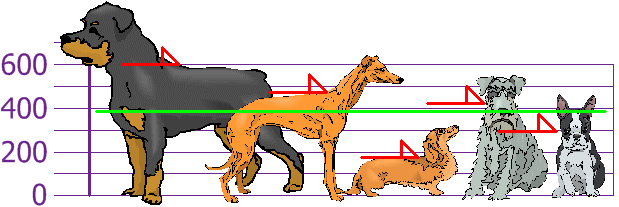
Ahora calculamos la diferencia de cada altura con la media:

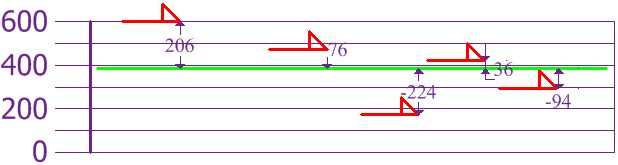
Para calcular la varianza, toma cada diferencia, elévala al cuadrado, y haz la media:

Varianza: σ² =	206² + 76² + (-224)² + 36² + (-94)²	=	108,520	= 21,704

	5		5

Así que la varianza es 21,704.

Y la desviación estándar es la raíz de la varianza, así que:

Desviación estándar: σ = √21,704 = 147

y lo bueno de la desviación estándar es que es útil: ahora veremos qué alturas están a distancia menos de la desviación estándar (147mm) de la media:

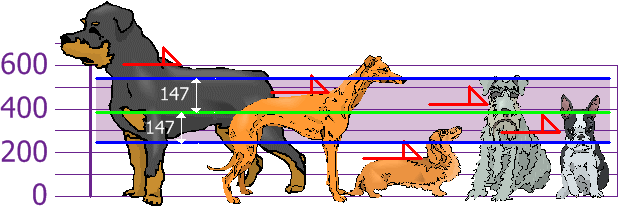
Así que usando la desviación estándar tenemos una manera "estándar" de saber qué es normal, o extra grande o extra pequeño.

Los Rottweilers son perros grandes. Y los Dachsunds son un poco menudos... ¡pero que no se enteren!

Nota: ¿por qué al cuadrado*?

Elevar cada diferencia al cuadrado hace que todos los números sean positivos (para evitar que los números negativos reduzcan la varianza)

Y también hacen que las diferencias grandes se destaquen. Por ejemplo 100²=10,000 es mucho más grande que 50²=2,500.